580 California St., Suite 400
San Francisco, CA, 94104
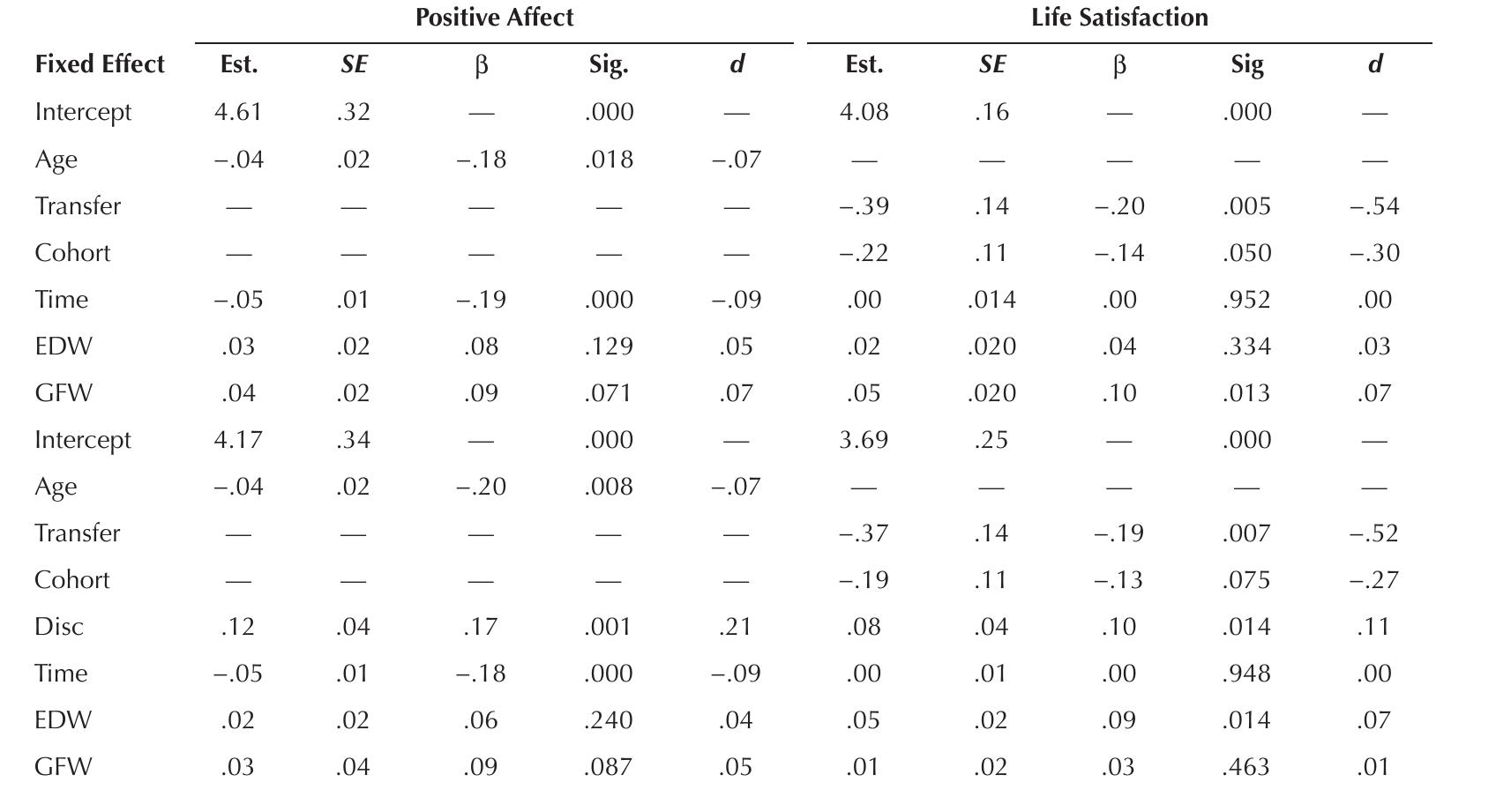
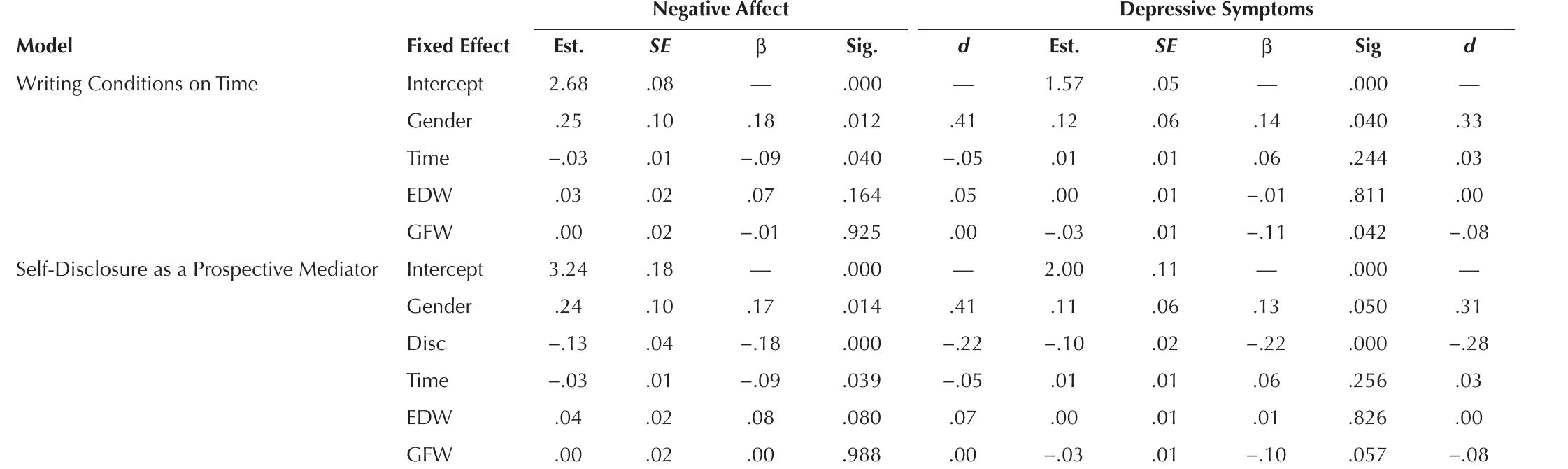
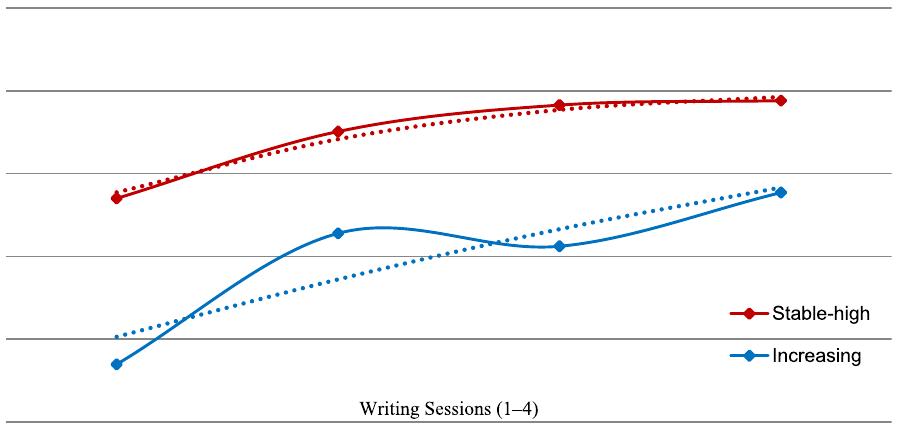
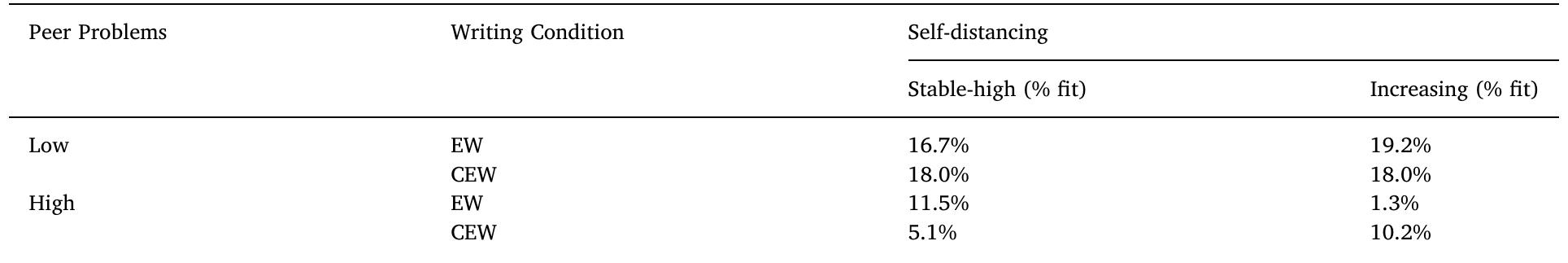Key research themes
1. How can direct collocation methods be effectively utilized and implemented for solving complex trajectory optimization problems in robotics and control?
This research theme focuses on the numerical techniques of trajectory optimization, especially direct collocation methods such as trapezoidal and Hermite–Simpson collocation. These methods transform continuous trajectory optimization into finite-dimensional nonlinear programs that can be solved efficiently. Their accessibility, implementation details, debugging strategies, and ability to handle complex robotic problems (such as bipedal walking and cart-pole swing-up) are critical for advancing practical trajectory planning.
Key finding: Provides a comprehensive tutorial on direct collocation methods for trajectory optimization, demonstrating how trapezoidal and Hermite–Simpson collocation can be effectively applied to solve a range of problems from simple... Read more
Key finding: Develops a neural network-based surrogate model trained on dynamic simulations to accelerate the evaluation of vehicle dynamics during trajectory optimization, thus addressing the computational bottleneck in nonlinear... Read more
Key finding: Combines nonlinear Model Predictive Control (NMPC) with Sampled-Data Control Barrier Functions to safely track time-varying trajectories within a corridor of permissible error, ensuring continuous-time safety and practical... Read more
Key finding: Introduces a novel orientation planning primitive ensuring jerk-continuous and smooth rotational trajectories compatible with high-degree-of-freedom manipulators; the method overcomes the discontinuities caused by piecewise... Read more
2. How can uncertainty and variability in dynamic trajectories be modeled and integrated into trajectory prediction and planning frameworks, particularly in aviation and autonomous vehicles?
This theme concentrates on modeling and managing uncertainties that arise in trajectory prediction of dynamic agents such as aircraft or vehicles. It includes probabilistic representations of trajectory deviations due to environmental, operational, or system-induced uncertainties, data-driven emulation approaches for capturing spatial-temporal correlations, and adaptive sampling methods to quantify and reduce positional uncertainty. Such modeling is vital for safety-critical applications like air traffic management and advanced driver assistance systems, providing robustness and reliability.
Key finding: Proposes a cause-and-effect probabilistic model that integrates multiple interdependent uncertainties (e.g., take-off mass, atmospheric condition variability) affecting aircraft trajectories, allowing analytical and numerical... Read more
Key finding: Presents a Gaussian Process-based monotonic functional emulator that probabilistically models aircraft vertical climb trajectories, capturing epistemic uncertainty and ensuring physically consistent monotonic altitude... Read more
Key finding: Introduces an adaptive sampling methodology using error ellipses to represent spatial uncertainty between discrete trajectory points, enabling determination of an optimal sampling rate that ensures interpolation errors remain... Read more
Key finding: Proposes the use of locally weighted regression techniques to reconstruct continuous vehicle trajectories from noisy and incomplete position data, estimating instantaneous speeds and accelerations critical for microscopic... Read more
3. What symbolic and data-driven representations can be employed to extract semantic information and perform anomaly detection from raw geometric trajectories in movement analysis?
Research in this theme seeks to convert raw geometric trajectory data into higher-level semantic annotations or symbolic forms to enable advanced querying, interpretation, or anomaly detection. Approaches include symbolic trajectory models that annotate trajectories with meaningful labels or segmentations, machine learning methods (neural networks, autoencoders, neuro-fuzzy systems) for flexible anomaly detection, and mixtures of vector fields modeling trajectories as generated by distinct motion regimes. These methods enhance trajectory data usability in transportation, surveillance, and behavioral analysis.
Key finding: Develops TrImpute, a scalable trajectory imputation framework that inserts artificial GPS points to densify sparse trajectories without requiring knowledge or inference of an underlying road network; leveraging... Read more
Key finding: Proposes a hybrid anomaly detection framework combining convolutional neural networks, adaptive neuro-fuzzy inference systems, and autoencoder networks to detect abnormal traffic trajectories in video surveillance data; the... Read more
Key finding: Introduces a generative trajectory modeling approach using mixtures of vector (velocity) fields that characterize different motion regimes; by modeling trajectories as generated by one or concatenations of velocity fields... Read more