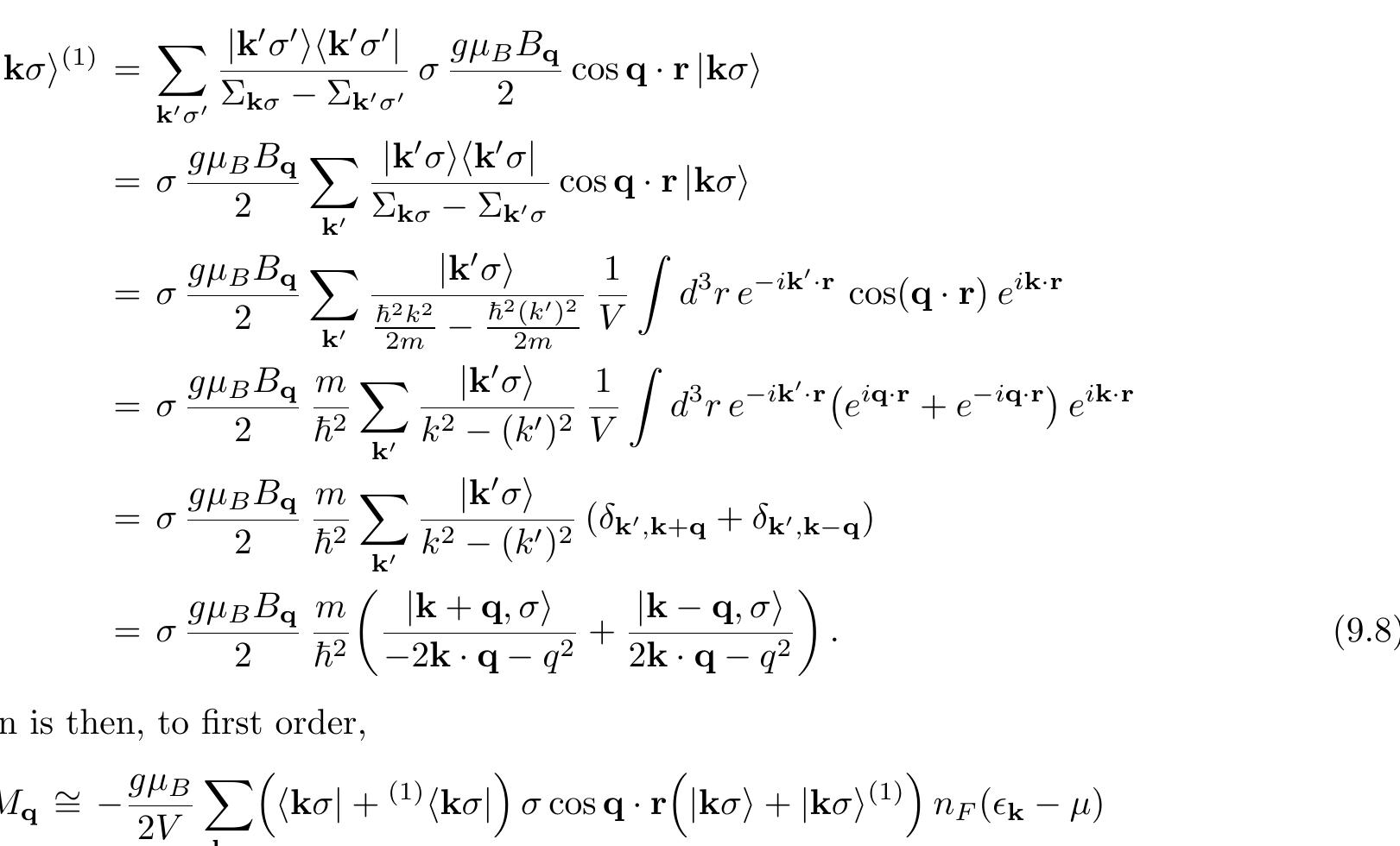The generalized decoration-iteration transformation is adapted for the exact study of a coupled spin-electron model on 2D lattices in which localized Ising spins reside on nodal lattice sites and mobile electrons are delocalized over... more
This paper presents an split-deflection method of classical rectangular plate analysis. In this method, the deflection was split into x and y components of deflection. It was assumed that the deflection of the rectangular plate is the... more
Structurally disordered s-d model of magnetism in metals is investigated. The simplified model of binary alloy structure is offered, the structural correlation functions are calculated. The self-consistent equations for calculation of a... more
Starting from an anisotropic super-exchange Hamiltonian as is found for compounds with strongly correlated electrons in multi-orbital bands and subject to strong spin-orbit interaction we calculate the contribution of thermal and quantum... more
Vibration analysis of line continuum with new matrices of elastic and inertia stiffness is introduced in this research. The matrices were developed using Ritz method and assumed six term Taylor's series shape function. Two deformable... more
We consider the case of electromagnetic field inside a rectangular cavity with conducting walls as a form of a system described by classical mechanics equations. We pass these equations through the Lagrangian formalism to obtain the... more
This paper presents an split-deflection method of classical rectangular plate analysis. In this method, the deflection was split into x and y components of deflection. It was assumed that the deflection of the rectangular plate is the... more
This work studied the buckling analysis of biaxially compressed all-round simply supported (SSSS) thin rectangular isotropic plates using the Galerkin's method. The study was limited to thin rectangular isotropic plates having aspect... more
The behavior of a buckled isotropic rectangular plate of Clamed-Simply-Free-Simple (CSFS) plate was critically examined in this paper; this was accomplished by truncating the polynomial series at the fifth orthogonal terms, which... more
This paper presents new approach to pure bending analysis of platforms with one clamped and three simply supported edges (SCSS and CSSS). Taylor-Mclaurin's polynomial shape function was derived and substituted into the Galerkin's... more
This paper presents buckling analysis of rectangular plate by split-deflection method. Here the deflection was taken as the product of these two components in x and y directions. The study formulated the total potential energy functional... more
This paper provides an efficient solution for determining very good a approximate solutions to the CSCS and SCSC platform problems i.e. platforms with two opposite edges clamped and two opposite edges simply supported. Taylor-Mclaurin's... more
All the previous studies on buckling and postbuckling loads of plate having all four edges simply supported (SSSS) have been limited to the use of assumed double trigonometric functions of displacement and stress. This has constrained... more
All the previous studies on buckling and postbuckling loads of plate having all four edges simply supported (SSSS) have been limited to the use of assumed double trigonometric functions of displacement and stress. This has constrained... more
This paper presents deflection function for plate analysis in the form product of two mutually perpendicular truncated polynomial series. The aim herein is to adopt this function as a very good approximate deflection function for first... more
This paper presents use of variational calculus to evolve third order functionals for continuum analysis. The governing equilibrium equation of forces of a line continuum was integrated in the open domain with respect to deflection to... more
This work deals with buckling analysis of a three dimensional isotropic thick plate clamped in all the edges (CCCC) subjected to a uniaxial compressive load, using the variational Energy method. Total potential energy equation of a thick... more
This work deals with buckling analysis of a three dimensional isotropic thick plate clamped in all the edges (CCCC) subjected to a uniaxial compressive load, using the variational Energy method. Total potential energy equation of a thick... more
The broadening of the density of magnetic-impurity-spin states, in a dilute magnetic alloy, is discussed. It is shown that the Ruderman-Kittel-Kasuya-Yosida (RKKY} interaction between the impurities can account for such a broadening. The... more
This paper presents exact approach to buckling analysis of SSSS and CCCC thin rectangular plates under vibration using split-deflection method. In this method, deflection function, is split into . Total potential energy functional for a... more
This paper presents exact approach to buckling analysis of SSSS and CCCC thin rectangular plates under vibration using split-deflection method. In this method, deflection function, is split into . Total potential energy functional for a... more
This paper presents exact approach to buckling analysis of SSSS and CCCC thin rectangular plates under vibration using split-deflection method. In this method, deflection function, is split into. Total potential energy functional for a... more
This paper presents a new, simple and exact approach to post-buckling analysis of thin rectangular plates. In the study, the Airy's stress functions are not incorporated as the middle surface axial displacement equations are determined as... more
One of the major problems of rectangular platebuckling under in-plane load is the rigorous approach use in its analysis. In this study, the problem of buckling was addressed by developing a Matlab based computer program for ease of... more
Two thin rectangular plates, one simply supported on all sides (SSSS), and the other plate simply supported and fixed on alternate opposite sides(CSCS), were analyzed for buckling or stability. Polynomial series were used to formulate... more
This paper presents use of variational calculus to evolve third order functionals for continuum analysis. The governing equilibrium equation of forces of a line continuum was integrated in the open domain with respect to deflection to... more
This paper presents an split-deflection method of classical rectangular plate analysis. In this method, the deflection was split into x and y components of deflection. It was assumed that the deflection of the rectangular plate is the... more
Spin-electron exchange model is generalized and used for description of magnetic states of amorphous substitutional alloys with the structural disorder of the liquid type. A scheme of consistently accounting for the contributions of... more
A general method for obtaining the oscillation periods of the interlayer exchange coupling is presented. It is shown that it is possible for the coupling to oscillate with additional periods beyond the ones predicted by the RKKY theory.... more
A new approach to the analysis of S-S short cylindrical shells subject to internal hydrostatic pressure is presented. Short cylindrical shells with both ends simply supported (S-S) loaded with axisymmetric internal hydrostatic pressure... more
The use of polynomial series function in the buckling analysis of a CCFC is presented. The polynomial series shape function was truncated at the fifth orthogonal terms, which satisfied all the boundary conditions of the plate to obtain a... more
The traditional approach in the analysis of axisymmetrically loaded short cylindrical shells has been to solve the fourth order differential equation using the Krylov's equation. This involved a transition from exponential functions to... more
The use of polynomial series function in the buckling analysis of a CCFC is presented. The polynomial series shape function was truncated at the fifth orthogonal terms, which satisfied all the boundary conditions of the plate to obtain a... more
The work is to use the energy approach in the form of indirect variational principle (Galerkin's method) for buckling analysis elastic of thin rectangular plates with all edges clamped. The Galerkin method has been used to solve problems... more
This study considers the application of characteristic orthogonal polonomial to Galerkin indirect variational method for buckling analysis elastic of thin rectangular plates with all edges simply supported. The Galerkin method has been... more
This paper studied the stability analysis of orthotropic reinforced concrete shear wall panel with all edges simply supported by the application of Ritz method. The study was carried out through a theoretical formulation based on applying... more
Using first-principles density-functional-theory-based calculations, we analyze the structural stability of small clusters of 3d late transition metals. We consider the relative stability of the two structures: layer-like structures with... more
A self-consistent approach is applied for the calculations within the two-time temperature Green functions formalism in the random phase approximation. The effective mass of 4 He atom is computed as m * = 1.58 m. The excitation spectrum... more







![This makes it difficult to some analysts in obtaining orthogonal function for a plate of a particular boundary condition. Recently, some scholars have applied split-deflection method in buckling analysis of some plates of particular boundary conditions but did not consider the effect of vibration on it. Ibearugbulem et al. 14] applied split-deflection method in buckling analysis of CCSS and CCCS thin rectangular plates under vibration. From the existing literatures, none has considered buckling analysis of SSSS and CCCC thin rectangular plates under vibration. Thus, this paper used trigonometric-polynomial deflection function in split form to solve the buckling problems of SSSS and CCCC thin rectangular plates under vibration caused by ateral loads subjected on both sides at x-axis shown in Figures | & 2. The boundary conditions for SSSS plate at x-axis are:](https://figures.academia-assets.com/66057885/figure_001.jpg)










![2. TOTAL POTENTIAL ENERGY FUNCTIONAL FOR BUCKLING OF PLATE. Engineers and students can turn to for a clear and orderly exposition of the Isotropic rectangular plate with clamped - clamped - free - clamped edge subjected to dynamic boundary conditions, which are also known as non-essential boundary condition. Ibearugbulemsolved CCFC rectangular plate using Taylor - Mclaurin’s shape function with the aid of eigen value computer programme[6]. 11 ae Ibearugbulem [6] derived the total potential energy functional for a rectangular isotropic plate subjected to in- plane load in x - direction and the polynomial shape function as follows;](https://figures.academia-assets.com/34237871/figure_001.jpg)


![Thus, if a function w(x, y) is an exact solution of the given boundary value problem, then, the function [L(w) — N] will be orthogonal to any set of functions. Since the deflection function, wy(x,y) in the form of Equation 22.0 is an approximate solution only if Equation 20.0, [L(w) — N] + 0, and it is no longer orthogonal to any set of functions. However, requiring that the magnitude of the function [L(w) — N] be minimum. This requirement is equivalent to the condition that the above function should be orthogonal to some bounded set of functions: first of all, to the trial functions f,(x). It leads to the following Galerkin equation: In non — dimensional form,](https://figures.academia-assets.com/34114141/figure_001.jpg)



![where & is from the first Brillouin zone, k €]—7, 7]. For A ¥ 0 we find a nearest-neighbor density-density interaction. The model is still exactly solvable using the Bethe ansatz, but this solution is much more complicated than for A = 0. We know, however, that the ground state |0) is a spin singlet. Thus](https://figures.academia-assets.com/33543903/figure_044.jpg)

![This is, not surprisingly, the field of a magnetic dipole. We can thus identify m; with the magnetic dipole moment of the current loop. Tha. snanaetin (AGHA lAY) mranewant 4a fave] Writing unit vectors with a hat, A = a/a, we obtain Compare the orbital angular momentum of the electron: We had found 1 = m,R?w. We obtain the relation](https://figures.academia-assets.com/33543903/figure_001.jpg)
![In quantum physics, it is common to write angular momenta as dimensionless quantities by drawing out a factor of h. Thus we replace s > sh, s/h > s,m, > m, = —gyps etc. We use this convention from now on. The interaction of the electronic charge with the electromagnetic field it generates leads to small corrections (“anomalus magnetic moment”), which can be evaluated within QED to very high accurancy. One finds The derivation of the Pauli equation gives s-s = 3/4. We know from introductory quantum mechanics that any angular momentum operator L has to satisfy the commutation relations [L,, Li] = 1 >0,,, €kimLm, [Lx, L?] = 0, which define the spin algebra su(2). (These commutation relations are to a large extend predetermined by the commutation relations of rotations in three-dimensional space—a purely classical concept. This does not course not fix the value of h, though.) It is also shown there that this implies that L? can have the eigenvalues /(1 +1) with J = 0, 3 1, 3, 2,... and Ly, k = x,y, z, can than have the eigenvalues m=-—l,-l+1,...,0-1,1.](https://figures.academia-assets.com/33543903/figure_002.jpg)
























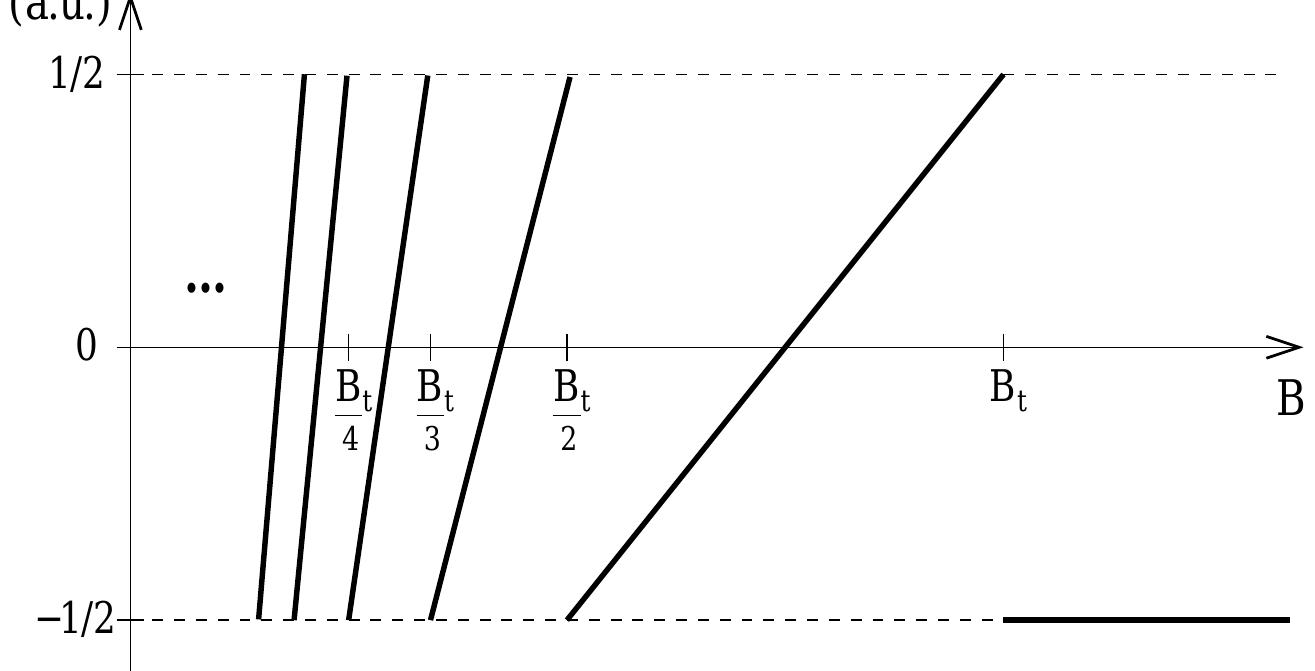
![Solutions correspond to intersections between the straight line M — M (the identity function) and the curv M > SBs(J(Q)M/kegT). A non-trivial solution exists if SBgs has a larger slope at M = 0 than the identit finction. j.e.. if for the unknown M € [0,S]. Since Bg(0) = 0, there is always a solution M = 0. Non-trivial solutions have to be found numerically or graphically. The mean-field approximation now amounts to solving the equation](https://figures.academia-assets.com/33543903/figure_028.jpg)
![YUCHULY, LAA YZ \UY)] -— U- To see that the non-trivial solution is the stable one, if it exists, one has to consider the free energy. The result within mean-field theory is that for T < T, the free energy has a minimum at M > 0 but a maximum at M = 0. Thus the average of J(q) is zero. If there is any exchange interaction, J(q) is not identically zero. Conse- quently, max J(q) > 0.](https://figures.academia-assets.com/33543903/figure_029.jpg)