Key research themes
1. How can persistent and low-latency shared memory be efficiently realized in distributed multiprocessor datacenter systems?
This theme investigates the integration of next-generation non-volatile memories (NVMs) into distributed shared memory (DSM) systems to provide a global persistent memory abstraction with low latency, reliability, and high availability in datacenter-scale multiprocessor environments. It matters because NVMs offer DRAM-like speeds combined with persistence and high density, which can significantly enhance large-scale application performance, persistence, and fault tolerance, but leveraging these benefits across distributed nodes requires novel system software and hardware designs.
2. What software and runtime techniques effectively manage scheduling, load balancing, and parallelism in shared-memory multiprocessor systems?
This theme focuses on dynamic scheduling approaches, task parallelism exploitation, and runtime mechanisms that optimize workload distribution and parallel execution on shared-memory multiprocessors. Efficient scheduling is essential to fully leverage the hardware parallelism, improve load balance, and increase application throughput in multiprocessor systems.
3. How can software-level memory management policies and algorithms mitigate memory contention and improve scalability in shared memory multiprocessors?
This theme studies operating system and hardware memory management strategies, including page allocation, memory bank partitioning, and transactional memory buffering, to reduce interference, contention, and coherence overhead in shared memory multiprocessors. These approaches aim to enhance throughput and energy efficiency by optimizing access to shared DRAM banks and maintaining cache coherence.
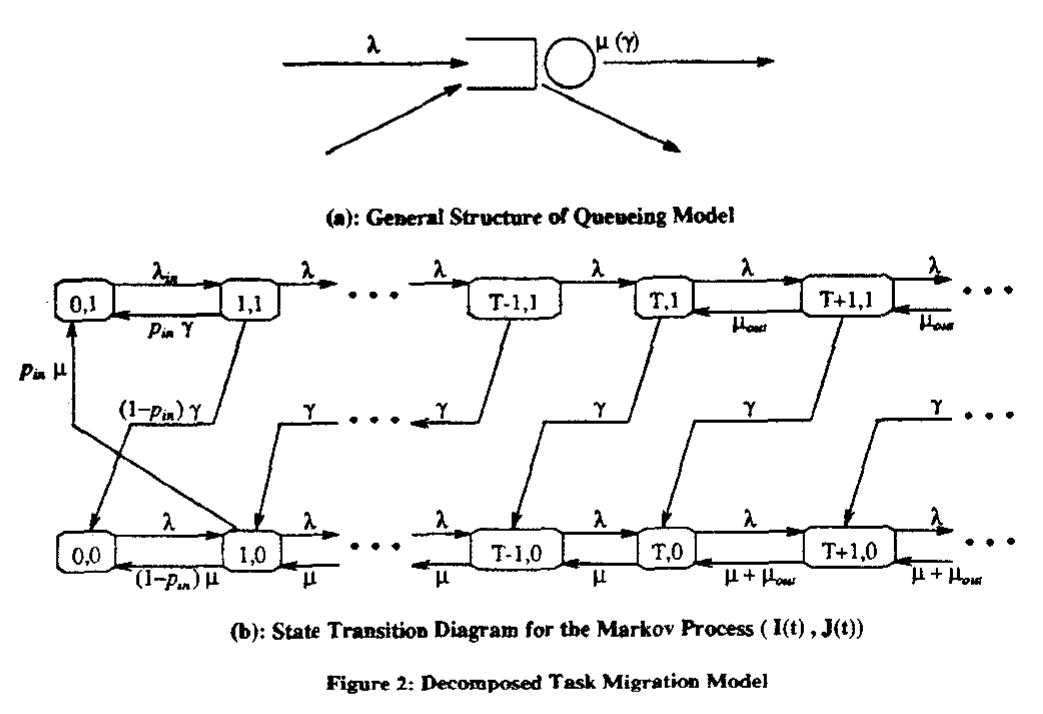
![where B o9, Bo, and B yo are finite matrices of dimensions OT x 2T, 2T x2 and 2x 27, respectively, whose elements depend upon the value of T. The remaining matrices have dimension 2 x 2 and are given by: Given this form for the generator matrix of the Markov process, the components of the steady state probability vector y can be obtained exactly via matrix-geometric techniques[20]. In particular, the geometric portion of the probability vector, representing when the processor is above threshold, can be solved as](https://figures.academia-assets.com/114046608/figure_003.jpg)