Key research themes
1. How can population-based metaheuristic algorithms effectively balance exploration and exploitation in complex optimization problems?
This research area focuses on developing and improving population-based metaheuristic optimization algorithms to effectively navigate complex, nonlinear, and multimodal search spaces. A central challenge is achieving a suitable balance between exploration (diversifying search across the solution space) and exploitation (intensifying search near promising areas). Efficient balancing improves convergence speed, avoids local optima, and enhances solution quality for a broad class of problems, including engineering design and real-world applications.
2. What are best practices and key considerations in implementing optimization methods in statistical computing environments like R?
This theme centers on methodological insights and software implementation aspects of nonlinear parameter estimation and optimization methods within open-source statistical computing platforms, particularly the R environment. It addresses challenges of user-friendliness, default method choices, evolution and maintenance of optimization packages, the integration of legacy and modern algorithms, and developing a coherent, best-practice framework to enhance reliability and extensibility of optimization tools in applied statistics and scientific computing.
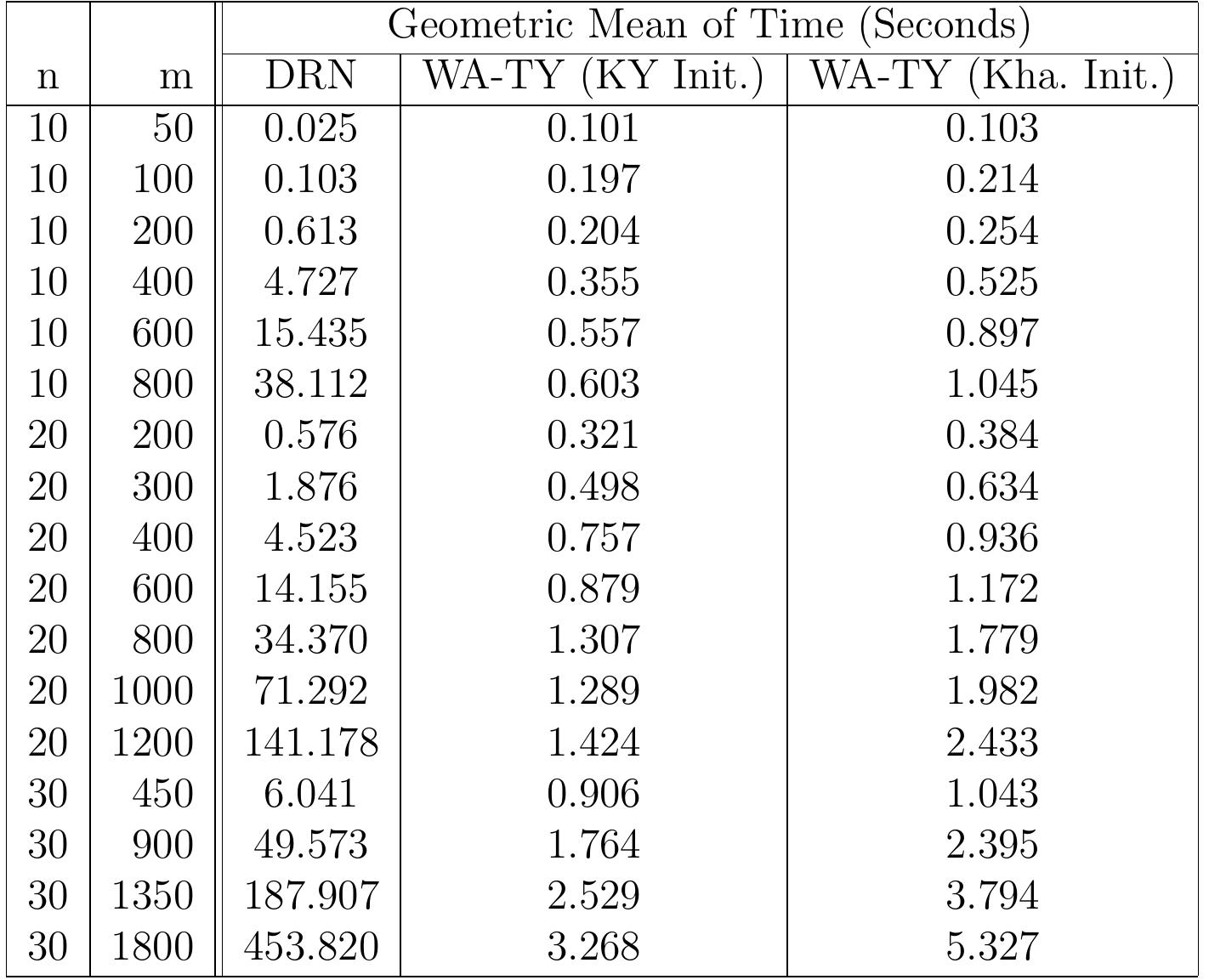
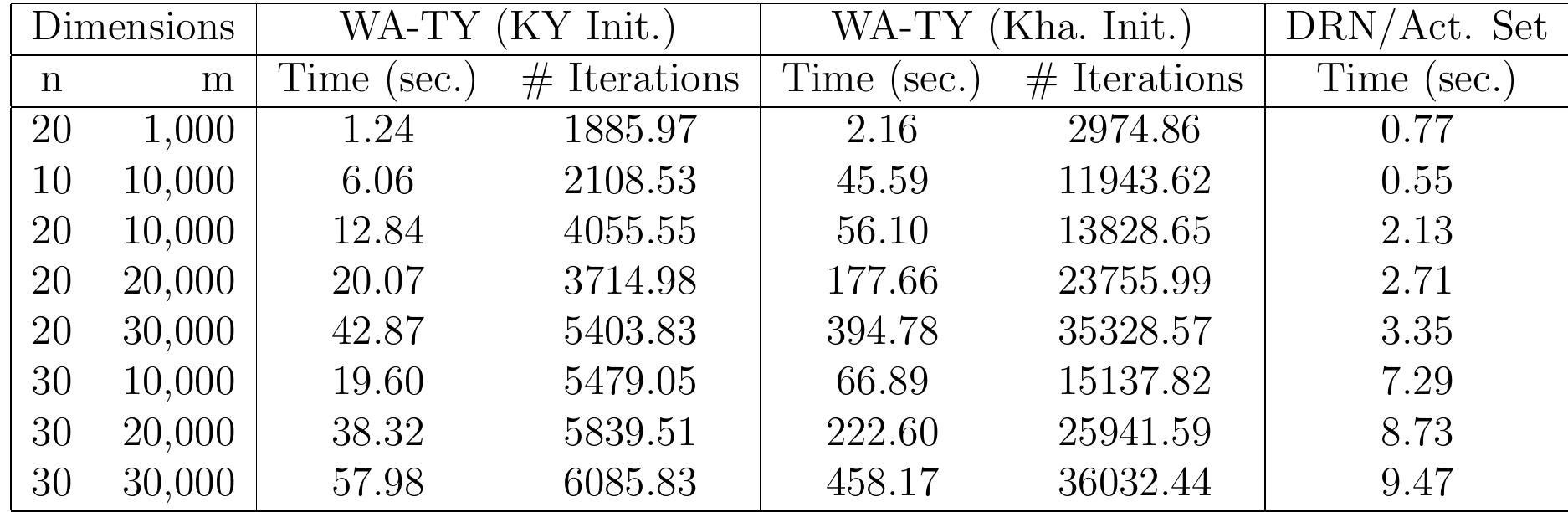
3. How do mathematical and computational advances address specific challenges in large-scale and nonlinear constrained optimization problems in engineering and applied sciences?
This theme explores advances in mathematical optimization techniques tailored for large-scale, nonlinear, and constrained problems prevalent in engineering applications, including numerical PDEs, linear programming interior point methods, batch plant design, and resource optimization in construction project management. It focuses on algorithmic innovations such as improved gradient methods, preconditioning strategies, and hybrid deterministic/stochastic approaches to enhance computational efficiency, convergence guarantees, and practical applicability in complex systems.