The initial data in the polygon approach to (2+1)D gravity coupled to point particles are constrained by the vertex equations and the particle equations. We establish the hyperbolic nature of the vertex equations and derive some... more
This article introduces a new class of multivariate Hermite-Frobenius-Genocchi polynomials and explores various characterizations of these polynomials. We examine their properties, including recurrence relations and shift operators. Using... more
The paper presents evidence that Riemann's ξ function evaluated at 2 √ E could be the characteristic function P (E) for the magnetic Laplacian minus 85 16 on a surface of curvature −1 with magnetic field 9 4 , a cusp of width 1, a... more
There exists an intriguing relation between genus zero correlation functions in the H + 3 WZNW model and in Liouville field theory. We provide a path integral derivation of the correspondence and then use our new approach to generalize... more
Antioxidants found in microalgae play an essential role in both animals and humans, against various diseases and aging processes by protecting cells from oxidative damage. In this study, 26 indigenous tropical marine microalgae were... more
Your article is protected by copyright and all rights are held exclusively by Springer Science+Business Media, LLC, part of Springer Nature. This e-offprint is for personal use only and shall not be self-archived in electronic... more
Motivated by recent works on the connection between 2D quantum gravity and timelike Liouville theory, we revisit the latter and clarify some aspects of the computation of its partition function: we present a detailed computation of the... more
We define a three-dimensional quantum theory of gravity as the holographic dual of the Liouville conformal field theory. The theory is consistent and unitary by definition. The corresponding theory of gravity with negative cosmological... more
The correspondence between the semiclassical limit of the DOZZ quantum Liouville theory and the Nekrasov-Shatashvili limit of the $ \mathcal{N} = 2 $ (Ω-deformed) U(2) super-Yang-Mills theories is used to calculate the unknown accessory... more
In this work we discuss the holographic description of states in the Hilbert space of (2+1)-dimensional quantum gravity, living on a time slice in the bulk. We focus on pure gravity coupled to pointlike sources for heavy spinning... more
In this paper, we explore some extensions of multiple fixed point results for various distance spaces such as s-distance space, s,q-distance space, and balanced distance space. Some examples are also discussed for the elaboration of these... more
In this paper a class of conformal field theories with nonabelian and discrete group of symmetry is investigated. These theories are realized in terms of free scalar fields starting from the simple b − c systems and scalar fields on... more
We develop analytical methods for computing the structure constant for three heavy operators, starting from the recently proposed hexagon approach. Such a structure constant is a semiclassical object, with the scale set by the inverse... more
In this paper, we use the idea of normal family to investigate the problem of meromorphic function having finitely many poles that share entire functions IM with its first derivative.
In this paper, we use the idea of normal family to investigate the problem of meromorphic function having finitely many poles that share entire functions IM with its first derivative.
Using conformal field theory and localization tecniques we study the propagation of scalar waves in gravity backgrounds described by Schrödinger like equations with Fuchsian singularities. Exact formulae for the connection matrices... more
We explore celestial amplitude corresponding to 2d bulk $$ \mathcal{S} $$ S -matrix. We consider scalar particles with identical mass and show that the celestial amplitude becomes the fourier transform of the 2d$$ \mathcal{S} $$ S -matrix... more
This paper studies the motion of an infinitesimal particle near the out-of-plane equilibrium points in the elliptic restricted three body problem when the primaries are triaxial rigid bodies, sources of radiation and surrounded by a belt.... more
This paper addresses an investigation on a factorization method for difference equations. It is proved that some classes of second order linear difference operators, acting in Hilbert spaces, can be factorized using a pair of mutually... more
Recently, a model equation that describes nonlinear heat waves in a rigid thermal conductor has been derived. The system of the governing equations for temperature and heat flux is nonlinear. The objective of the present work is to find a... more
Title: Lie groups of partial differential equations and their application to the multidimensional screening problems Date:
In this paper I described group theoretic methods that can be used for analyzing the boundary problems, which arise when the Hamiltonian method is applied to solve the relaxed problem for the multidimensional screening problem. This... more
We present some new results on the rational solutions of the Knizhnik-Zamolodchikov (KZ) equation for the four-point conformal blocks of isospin I primary fields in the SU (2) k Wess-Zumino-Novikov-Witten (WZNW) model. The rational... more
We continue the investigation of massive integrable models by means of the bootstrap fusion procedure, started in our previous work on O(3) nonlinear sigma model. Using the analogy with SU(2) Thirring model and the O(3) nonlinear sigma... more
Partially coherent image formation theory for a full-field imaging microscope is introduced. Propagation of mutual coherence is presented following Huygens-Fresnel principle. The concept of mutual intensity, together with the... more
Semiclassical Einstein equations are used to describe the interaction of the back-reaction of the classical gravitational field with quantum matter fields in semiclassical gravity. We in our previous studies have made use of the... more
Our main goal in this present paper is to define first a new extension of the Pochhammer symbol and the gamma functions which involving the Mittag-Leffler function in their kernels. By using this extended Pochhammer symbol, we then... more
Recently, a model equation that describes nonlinear heat waves in a rigid thermal conductor has been derived. The system of the governing equations for temperature and heat flux is nonlinear. The objective of the present work is to find a... more
Abstract. We give an explicit expression for the M-point correlator of the superconformal current in two dimensional N = 1 superconformal field theories. Correlators of N = 1 Superconformal Currents 2 1. Main Result N = 1 superconformal... more
A two-parametric family of integrable models (the SS model) that contains as particular cases several well known integrable quantum field theories is considered. After the quantum group restriction it describes a wide class of integrable... more
A cama de galpões de confinamento de bovino leiteiro no modelo compost barn tem grande impacto na qualidade e produtividade animal. O objetivo deste estudo é desenvolver um modelo não-linear para estimar a quantidade de bactéria em camas... more
We consider three models (elliptic, flat and hyperbolic) of Gaussian random analytic functions distinguished by invariance of their zeroes distribution. Asymptotic normality is proven for smooth functionals (linear statistics) of the set... more
Liouville field theory on a sphere is considered. We explicitly derive a differential equation for four-point correlation functions with one degenerate field V − mb 2. We introduce and study also a class of four-point conformal blocks... more
Expectation propagation is a general approach to fast approximate inference for graphical models. The existing literature treats models separately when it comes to deriving and coding expectation propagation inference algorithms. This... more
Multi-collinear factorization limits provide a window to study how locality and unitarity of scattering amplitudes can emerge dynamically from celestial CFT, the conjectured holographic dual to gauge and gravitational theories in flat... more
In recent years, several interesting families of generating functions for various classes of hypergeometric functions were investigated systematically. In the present paper, we introduce a new family of extended Wright type hypergeometric... more
We study co-dimension two monodromy defects in theories of conformally coupled scalars and free Dirac fermions in arbitrary d dimensions. We characterise this family of conformal defects by computing the one-point functions of the... more
ABSTRACT. Let pn be the number of partitions of an integer n. For each of the partition statistics of counting their parts, ranks, or cranks, there is a natural family of integer polynomials. We investigate their asymptotics and the... more
A cama de galpões de confinamento de bovino leiteiro no modelo compost barn tem grande impacto na qualidade e produtividade animal. O objetivo deste estudo é desenvolver um modelo não-linear para estimar a quantidade de bactéria em camas... more
In this paper, we obtain a (p, q)-extension of Srivastava's triple hypergeometric function H B (•), by using the extended Beta function B p,q (x, y) introduced by Choi et al. [Honam Math. J., 36 (2011) 357-385]. We give some of the main... more
We show that in boundary CFTs, there exists a one-to-one correspondence between the boundary operator expansion of the two-point correlation function and a power series expansion of the layer susceptibility. This general property allows... more
Multi-collinear factorization limits provide a window to study how locality and unitarity of scattering amplitudes can emerge dynamically from celestial CFT, the conjectured holographic dual to gauge and gravitational theories in flat... more
We show that the Lee-Pomeransky parametric representation of Feynman integrals can be understood as a solution of a certain Gel'fand-Kapranov-Zelevinsky (GKZ) system. In order to define such GKZ system, we consider the polynomial obtained... more
An interlayer phase coherence develops spontaneously in the bilayer quantum Hall system at the filling factor ν =1. On the other hand, the spin and pseudospin degrees of freedom are entangled coherently in the canted antiferromagnetic... more
We compute four-point functions in the Heavy-Heavy-Light-Light limit involving all possible 1/8-BPS heavy states whose dual supergravity solutions are explicitly known, avoiding the use of Witten diagrams. This is achieved by using the... more
We extend the semiclassical study of the Neumann model down to the deep quantum regime. A detailed study of connection formulae at the turning points allows to get good matching with the exact results for the whole range of parameters.
We present a rigorous proof of the Dorn, Otto, Zamolodchikov, Zamolodchikov formula (the DOZZ formula) for the 3 point structure constants of Liouville Conformal Field Theory (LCFT) starting from a rigorous probabilistic construction of... more
We show that logarithmic conformal field theories may be derived using nilpotent scale transformation. Using such nilpotent weights we derive properties of LCFT's, such as two and three point correlation functions solely from... more
In this paper we study two-dimensional (2D) convolutional codes which are obtained from series concatenation of two 2D convolutional codes. In this preliminary work we confine ourselves to dealing with finite-support 2D convolutional... more
Isomonodromy for the fifth Painlevé equation P5 is studied in detail in the context of certain moduli spaces for connections, monodromy, the Riemann–Hilbert morphism, and OkamotoPainlevé spaces. This involves explicit formulas for Stokes... more

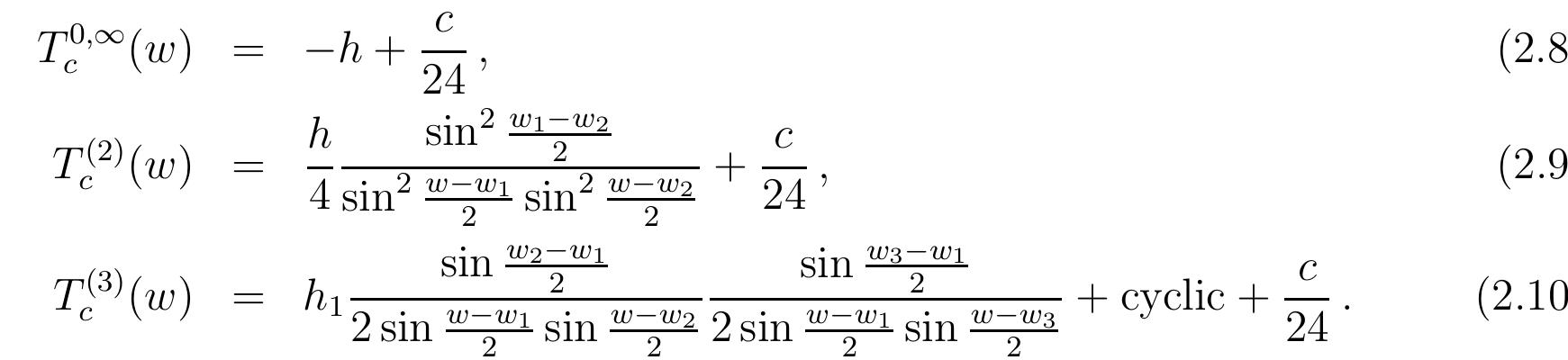
![where the symbol 2F\ stands for the hypergeometric function 2F, with arguments 2Fi(m + 3 — T2,m +72 +73 —1,2m,x). Using the differential equation the hypergeometric function In this appendix, we demonstate explicitly that the semiclassical limit of the energy-momentum tensor in the presence of three insertions is given by formula (4.25), as it must be. The energy- momentum tensor of Liouville theory in the semiclassical limit is [38]](https://figures.academia-assets.com/107804064/figure_002.jpg)


![Figure 1. Bulk S-matrix mapped to Boundary Celestial CFT correlation function. The motivation for seeking this conformal basis is to understand the holographic na- ture of quantum gravity in asymptotically flat spacetimes. Realization of the holographic duality [4-6] from the bottom up by finding the symmetries that both sides of the holo- graphic dual pair obey [14, 15] gives rise to the enhancement of the Lorentz symmetry to full Virasoro [16] and the existence of a stress tensor in a 2d CFT obeying Ward identity constructed from subleading soft-graviton mode in the bulk [17]. These observations along with the equivalence between soft theorems and asymptotic symmetries i.e., soft theorems recasted as conservation laws associated with large gauge symmetries lead to the proposal that there exists a holographic duality between the theory of gravity in four-dimensional asymptotically flat spacetimes and some sort of exotic CFT living on the two-dimensional celestial sphere at null infinity.](https://figures.academia-assets.com/100657832/figure_001.jpg)




![where 4 is a parameter of the model. This is a consistent S-matrix if 0 < » < 1/2; otherwise, there are poles insid the physical sheet 0 < Im@ < a. In [17] the one-loop renormalized action can be found. For our considerations w will need only the S-matrix (2.14). The S-matrix of the sausage-model is SU(2), invariant with gq = exp[ia(A + 1)]. When we set » > 0, we fin the S-matrix of the O(3) nonlinear sigma model. One can introduce the ZF operators Z;(/3) for the sausage mode similarly to the case of sine-Gordon theory. The basis needed to exhibit the quantum group symmetry is given by](https://figures.academia-assets.com/94955897/figure_001.jpg)








![Figure 1. Polytope of b(z) = 14 2, + z2 + cz, 22. Written as intersection of half planes, we have Ay = {a1 > 0} N {a2 > OF} N { 01 => inf 02> 1}. Let us now review the concept of a coamoeba of a variety. Consider the ideal J generated by some polynomials f;,..., f; C C[z1,...,2n]. The zero set of the ideal J = (fi,..., fj) defines the algebraic variety](https://figures.academia-assets.com/83096417/figure_001.jpg)
![Figure 2. Coamoeba (shaded) of b = 1+ 222 + 2123 + 2725 + caz7z drawn in the fundamental domain [—7,7] x [—7,7] of T? in R?. This case corresponds to c = (1,1,1,1,c4), with cy near 1. Here, we have three connected components, one of which contains (0,0) (center of the figure).](https://figures.academia-assets.com/83096417/figure_002.jpg)
![Figure 3. A connected component of the coamoeba(shaded) of b(z) = 1+ 21 + zg + cz122 drawn it the fundamental domain [—7,7] x [—7,7] of T? in R?. The coefficient ¢ is near 1.](https://figures.academia-assets.com/83096417/figure_003.jpg)








