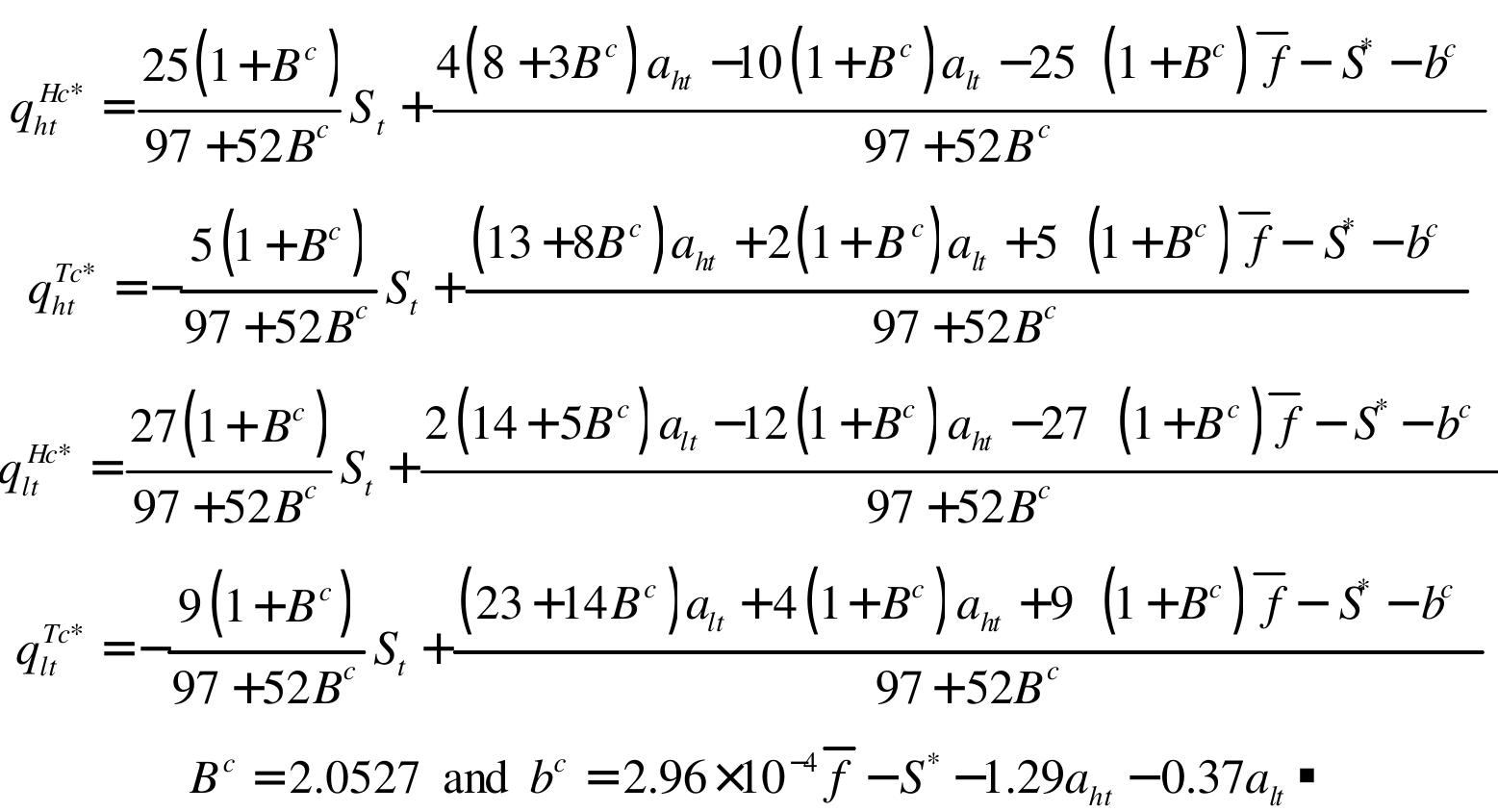This paper considers the optimal toll design problem that uses the Probit model to determine travellers' route-choices. Under probit, the route flow solution to the resulting stochastic user equilibrium (SUE) is unique and can be stated... more
The Network Design Problem (NDP) refers to the optimization problem faced by a planner whose aim is to improve a transport network, drawing on limited resources. Though the NDP may lead to, for example, a set of tolls that maximise social... more
Selfish routing, represented by the User-Equilibrium (UE) model, is known to be inefficient when compared to the System Optimum (SO) model. However, there is currently little understanding of how the magnitude of this inefficiency, which... more
In this paper we consider the question of solving equilibrium problems-formulated as complementarity problems and, more generally, mathematical programs with equilibrium constraints (MPECs)-as nonlinear programs, using an interior-point... more
In this work, the open loop dynamic optimisation of a large-scale natural gas processing plant is performed. A rigorous differential-algebraic equation (DAE) model has been formulated to represent main plant units, such as shell and tube... more
For an arbitrary finite family of semi-algebraic/definable functions, we consider the corresponding inequality constraint set and we study qualification conditions for perturbations of this set. In particular we prove that all positive... more
Chance constraints are a valuable tool for the design of safe decisions in uncertain environments; they are used to model satisfaction of a constraint with a target probability. However, because of possible non-convexity and... more
Chance constraints are a valuable tool for the design of safe decisions in uncertain environments; they are used to model satisfaction of a constraint with a target probability. However, because of possible non-convexity and... more
Deregulated electricity markets use an auction mechanism to select offers and their power levels for energy and ancillary services. A settlement mechanism is then used to determine the payments resulting from the selected offers.... more
Multi-leader multi-follower games are a class of hierarchical games in which a collection of leaders compete in a Nash game constrained by the equilibrium conditions of another Nash game amongst the followers. The resulting equilibrium... more
This note considers alternative methods for computing Wadropian (traffic network) equilibria using a multicommodity formulation in nonlinear program and complementarity formats. These methods compute exact equilibria, they are efficient... more
The convergence of many proximal algorithms involving a gradient descent relies on its Lipschitz constant. To avoid computing it, backtracking rules can be used. While such a rule has already been designed for the forward-backward... more
Complementarity models can represent the simultaneous optimization problems of one or several interacting decision-makers, and thus they have become an increasingly important and powerful tool for formulating and solving bottom-up energy... more
The paper concerns a new class of optimization-related problems called Equilibrium Problems with Equilibrium Constraints (EPECs). One may treat them as two level hierarchical problems, which involve equilibria at both lower and upper... more
Mathematical programs with equilibrium constrains (MPECs) in which the constraints are defined by a parametric variational inequality are considered. Recently, nonlinear programming solvers have been used to solve MPECs. Smoothing... more
Keywords: UCL Reference EPFL-CONF-158627 Record created on 2010-11-25, modified on 2016-08-09
The generalized higher order macroscopic traffic flow model is reformulated in the Lagrangian coordinate system to develop more efficient numerical method. Providing a new node model based on the Lagrangian coordinate system which is... more
This paper illustrates how a supplier profit may be affected by the market pricing mechanism under imperfect competition. A parameterized Supply Function Equilibrium (SFE) model involving manipulation of the sole intercept is used to... more
This paper proposes a frequency based transit assignment model that accounts for online information and strict capacity constraints. A heuristic is proposed to solve the problem, which first applies an unconstrained transit assignment... more
Transportation planners and traffic engineers are faced nowadays with immense modeling challenges arising from several emerging policy, planning, and engineering developments. In fact, the recent emergence of mobile sensing and traffic... more
Transportation planners and traffic engineers are faced nowadays with immense modeling challenges arising from several emerging policy, planning, and engineering developments. In fact, the recent emergence of mobile sensing and traffic... more
In this paper, we consider dynamic congestion pricing in the presence of demand uncertainty. In particular, we apply a robust optimization (RO) approach based on a bi-level cellular particle swarm optimization (BCPSO) to optimal... more
This work ia subject to copyright. All rights are reserved, whether the whole or part of the material ia concerned, Ipecifica1\y the filhts of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on... more
Approximately twenty years ago the modern interest for hierarchical programming was initiated by J. Bracken and J.M. McGill [9], [10]. The activities in the field have ever grown lively, both in terms of theoretical developments and terms... more
Complementarity models can represent the simultaneous optimization problems of one or several interacting decision-makers, and thus they have become an increasingly important and powerful tool for formulating and solving bottom-up energy... more
This paper is concerned with adaptive signal control problems on a road network, using a link-based kinematic wave model (Han et al., 2012). Such a model employs the Lighthill-Whitham-Richards model with a triangular fundamental diagram.... more
This paper is concerned with a dynamic traffic network performance model, known as dynamic network loading (DNL), that is frequently employed in the modeling and computation of analytical dynamic user equilibrium (DUE). As a key component... more
This paper is concerned with highway traffic estimation using traffic sensing data, in a Lagrangian-based modeling framework. We consider the Lighthill-Whitham-Richards (LWR) model (Lighthill and Whitham, 1955; Richards, 1956) in... more
Dynamic user equilibrium (DUE) is the most widely studied form of dynamic traffic assignment (DTA), in which road travelers engage in a non-cooperative Nash-like game with departure time and route choices. DUE models describe and predict... more
To optimize revenue, service firms must integrate within their pricing policies the rational reaction of customers to their price schedules. In the airline or telecommunication industry, this process is all the more complex due to... more
"Revenue optimization in energy networks involving self-scheduled demand and a smart grid" Forthcoming, Computers and Operations Research 134 (2021) 2. M. Zimmermann, E. Frejinger and P. Marcotte "A strategic Markovian traffic equilibrium... more
We study the Demand Adjustment Problem (DAP) associated to the urban traffic planning. The framework for the formulation of the DAP is mathematical programming with equilibrium constraints. In particular, if we consider the optimization... more
We consider a liberalized electricity market, divided in zones interconnected by capacitated transmission links, where a large dimensional power producer operates. We introduce a model for determining the optimal bidding strategies of the... more
By using a hypothetical transport network that reflects common origin and destination relations in a regional transport network, we illustrate the effects of changing fares from a zonal to a distance-based structure. We take the zonal... more
Non-additive link cost functions are common and important for a range of assignment problems. In particular in transit assignment, but also a range of other problems path splits further need to consider node cost uncertainties leading to... more
Recently, simulation-based methods have been successfully used for solving challenging stochastic optimization problems and equilibrium models. Here we report some of the recent progress we had in broadening the applicability of so-called... more
In this note we give an elementary proof of the Fritz-John and Karush-Kuhn-Tucker conditions for nonlinear finite dimensional programming problems with equality and/or inequality constraints. The proof avoids the implicit function theorem... more
We consider equilibrium constrained optimization problems, which have a general formulation that encompasses well-known models such as mathematical programs with equilibrium constraints, bilevel programs, and generalized semi-infinite... more
We address the problem of developing optimal bidding strategies for an energy producer that participates in a day-ahead electricity market. The producer is assumed to have complete knowledge of the market's parameters, i.e., the demand... more
In this paper we study mathematical programs with equilibrium constraints (MPECs) described by generalized equations in the extended form 0 ∈ G(x, y) + Q(x, y), where both mappings G and Q are set-valued. Such models arise, in particular,... more
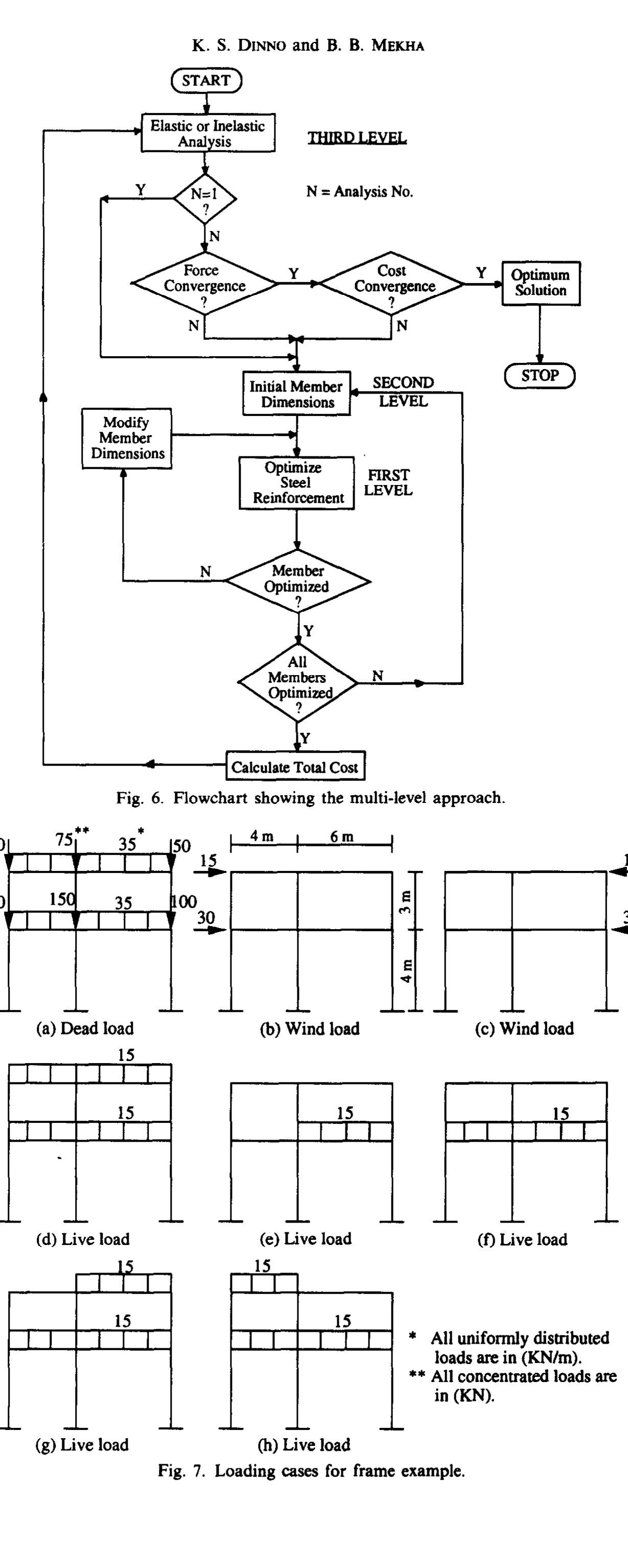
A new algorithm is presented for use in conjunction with the imposed rotation method as reformulated by Kaneko as a (n x 2n) linear complementarity problem. The inelastic trilinear moment rotation law, which is modelled to reflect... more
The planning of a rail transit system is a complex process involving the determination of station locations and the rail line alignments connecting the stations. There are many requirements and constraints to be considered in the planning... more
SOMMARIO : Si studiano atlraverso l'analisi limite le piastre coslituite di materiale rigido-plastico aventi superficie di snervamento di tipo poliedrico. I principi di eslremo riguardanti la vatutazione della potenza specifica di... more
This paper aims at studying a broad class of mathematical programming with non-differentiable vanishing constraints. First, we are interested in some various qualification conditions for the problem. Then, these constraint qualifications... more
In this paper, we study the difficult class of optimization problems called the mathematical programs with vanishing constraints or MPVC. Extensive research has been done for MPVC regarding stationary conditions and constraint... more
In this paper, we analyze infinite discrete-time games between hydraulic and thermal power operators in the wholesale electricity market. Two types of games are considered: Cournot closed-loop game and Stackelberg closed-loop game. W e... more
Demand response (DR) using shared energy storage systems (ESSs) is an appealing method to save electricity bills for users under demand charge and time-of-use (TOU) price. A novel Stackelberg-game-based ESS sharing scheme is proposed and... more
This document describes the models for network design and planning in the field of urban transportation that have been developed in the course of research project TRA2008-06782-C02-02. This includes transit, rapid transit and bus... more
![Definition 3.2 (Strong-stationarity point of P*°) A point (x,y) © F°° is a strong stationarity point of P** if there exist Lagrange multipliers n;, U4, ; and B;,t € N such that the following conditions hold: Having defined the strong stationarity conditions, we are now in a position to define the second-order sufficiency conditions. These assume relevance in defining a local Nash equilibrium; loosely speaking, at a local Nash equilibrium, every agent’s decision satisfies the mathematical programs with equilibrium constraints-second-order sufficiency or the MPEC-SOSC conditions, given the decisions of its competitors. Furthermore, Corresponding to a stationary point of P@®,, we may prescribe an active set A(x, y) such that A(«,y) * {Ai(a,y),...,An(,y)}, rnlp? where A. (x. y) denotes the set of active constraints corresponding to the set of constraints where [-]; denotes the j** component of ‘-’ and Ti, TE denote the complements of Tig, 1d respectively. Further, we refer to the both index sets collectively as Z; and the collection of index sets {Z;,...,Zy} by Z. Note that in accordance with [12], we define the index sets independent of the point (2, y). We may now state the strong stationarity conditions at a particular point (a, y).](https://figures.academia-assets.com/118245873/figure_001.jpg)
![Furthermore, (x,y) is a Nash second-order strong stationary point of &*° if (a,y) is a Nash strong station- ary point of &°° and if fori = 1,...,N, 8] Vin, yLi(@, Y)Si > 0 for 5; € S¥(x,y) where S¥(x,y) is given by (18), where Vi, y,Li denotes the Hessian of the Lagrangian function of Li*(2~*, y~*) with respect to (2%, yi) evaluated at (Lis Ys Mis Mis Ai, D piseg ie) if é" = &* or at (Ui, Yas Mi, His Ai, Bi) af Er € {goad gel or at (i, Yas Thi, His Ai, Vir Bi) Uf C88 = EX.](https://figures.academia-assets.com/118245873/figure_002.jpg)
![This is a generalized Nash game with coupled but not shared constraints. However, since the optimizatior problems of the leaders are convex (this is not obvious; see [33, Lemma 1] for a proof), we may use the first- order KKT conditions to derive an equilibrium. Let \; be the Lagrange multiplier corresponding the constraint ~~ a—b>); x; aay ip’ : Y= orb Pin The equilibrium conditions of this game are satisfies equilibrium conditions for the restricted game {Li}icv. The optimal Lagrange multiplier is given by AF = —nbx*, jv; = 0. It can then be verified that this equilibrium also satisfies the requirement }°;7* < a/b whereby it is an equilibrium of the original game. The other case of Y; = 0 does not result in an equilibrium tha‘ satisfies }>, 7; > a/b, and consequently «* is the only equilibrium.](https://figures.academia-assets.com/118245873/figure_003.jpg)
![equilibrium conditions for the generalized Nash equilibrium (see [18]) of this game are Notice that the Lagrange multipliers x for 7 £7 are unconstrained barring their presence in the first condition of (26). Comparing (26) and (25), we see that if A*,2* solve system (25), then 2 = a* and Be = MIpj=; for all i,j € N gives a solution to system (26). Consequently, an equilibrium of the original game & is an equilibrium of &°°. We have thereby verified Proposition 3.1 for this problem. The presence of surplus Lagrange multipliers provides us with more variables than the number of equations, whereby existence of solutions is easier to guarantee. An equilibrium of & is an equilibrium of the modified game &°° with a specific configuration of the vector of Lagrange multipliers. Consequently, if an equilibrium exists to &°©, there is no guarantee that there exists one to the original game &.](https://figures.academia-assets.com/118245873/figure_004.jpg)
![Hierarchical Cournot games: In a hierarchical Cournot game, leaders compete in a Cournot game and are constrained by the reactions of a set of followers that also compete in a Cournot game. We discuss a setting comprising of N leaders and M followers, akin to that proposed by Sherali [33]. Suppose the i‘? leader’s decision is denoted by x; and the follower strategies conjectured by leader 7 are collectively denoted by {yt He, where f denotes the follower index. Given the leaders’ decisions, follower f participates in a Cournot game in which it solves the following parametrized problem: where p(.) denotes the price function associated with the follower Cournot game, dep(yf )? denotes firm f’s quadratic cost of production, 7 = 0,2, 9 = >, yf, and yf & jz ¥’- Leader i solves the following parametrized problem:](https://figures.academia-assets.com/118245873/table_001.jpg)
![f € R is leader i’s conjecture of follower f’s equilibrium strategy, y; * {yf }41, 3dix? denotes the cost = {xj}jei and y~ uilibr multi-follower is given by {(xi,y:)}§_, where (2;, y:) is a solution of L;(a~*, y~*) for i=1,...,N. In this regime under identical leader costs, Sherali [33] proved the existence and uniqueness of the associated equilibrium. More recently, DeMiguel and Xu [4] extended this result to stochastic regimes wherein the price function is uncertain and the leaders solve expected-value problems. where y of production of leader i, x~* vs {yf 14; p—1- The equilibrium of the resulting multi-leader](https://figures.academia-assets.com/118245873/table_002.jpg)
![Spot-forward markets: Motivated by the need to investigate the role of forward transactions in power markets, there has been much interest in strategic models where firms compete in the forward market subject to equilibrium n the real-time market. Allaz and Vila [1] examined a forward market comprising of two identical Cournot firms und demonstrated that global equilibria exist in such markets. Su [37] extended these existence statements to . multi-player regime where firms need not have identical costs. In such an N-player setting, given the forward lecisions of the players {a;}+_,, firm i solves the following parametrized problem in spot-market: Yi,j 18 the where c¢;z; is the linear cost of producing z; units in the spot-market, 7 = )°> 57 and p(.) is the price function in the spot-market. In the forward market, firm i’s objective is given by its overall profit, which is given by —p! a; — p(¥i)(Yii — Li) + Cryii, Where p! denotes the price in the forward market Yi,7 is the anticipated equilibrium production by leader j and jj; = >> ; ¥ig- By imposing the no-arbitrage constraint that requires that p! = p(y), the forward market objective reduces to c;yi,i — p(¥i)yii- Firm i’s problem in the forward market is given by the following:](https://figures.academia-assets.com/118245873/table_003.jpg)

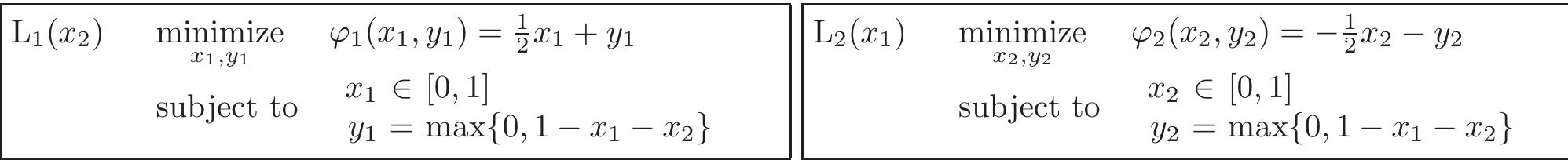
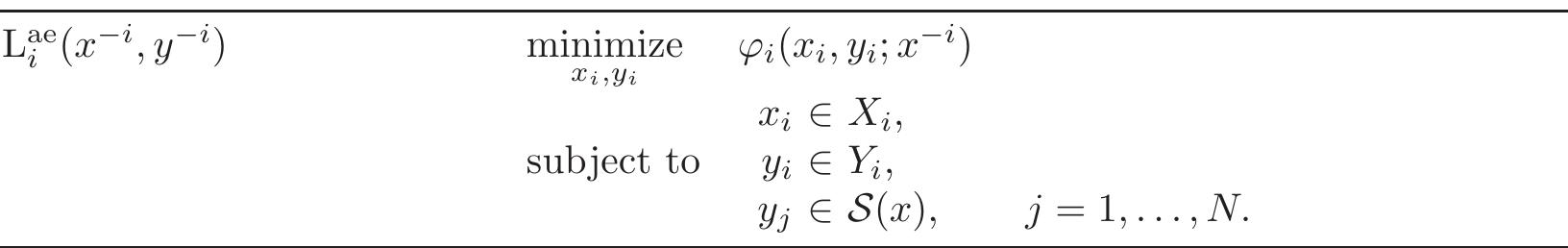
![A special case of the conventional game & which is already a shared-constraint game is the case (denoted by &>!) where leaders have disjoint set of followers. Effectively, each leader solves bilevel optimization problems a follows. Since y; € §; (2), there is no coupling of leader decisions in the constraints of leader problems. This is a special case of & with S(x) = []j< a Se (a;), where S; (x;) is the solution of a variational inequality for each 7 and where the objective of leader i depends only on the equilibrium of S; (xi) and not on S; (x;) for 7 £ 7. With a slight abuse of our notation so far, we let y; denote an element of the set S. (x;) and Y; be the apaiae of such y;. Let OF be the feasible region of L?!(a~*, y~*) and let F°! be the set of fixed points of >! + mW, QP. Since there is no coupling, it is easily seen that](https://figures.academia-assets.com/118245873/table_007.jpg)

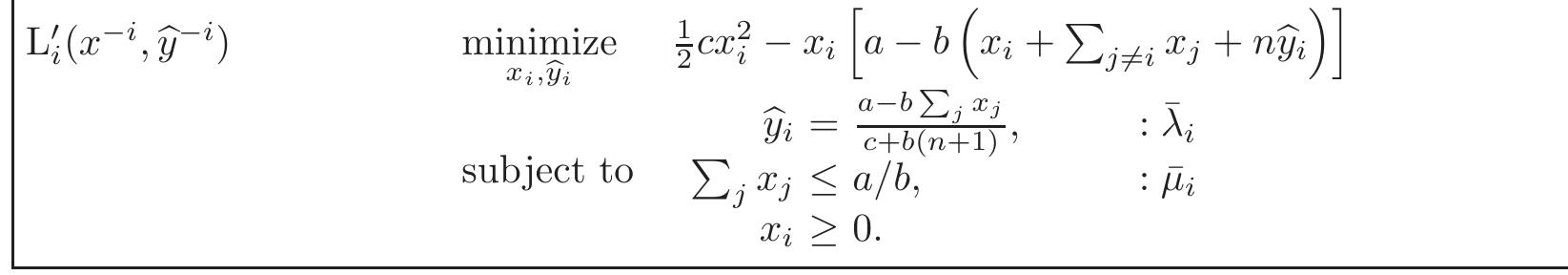
![Verifying Proposition 3.1 (An equilibria of & is an equilibrium of &*°): Let us now consider this game modified as €°°. Notice that the equilibrium constraint is now for all f and for all k. For any k, the equilibrium constraint may be simplified using (24), giving an equation in Y,. It is easy to check that this game also admits no equilibrium with >?,2; > a/b. Thus, this game is equivalent to the game where >’, 2; is constrained to be in [0,a/b]. For such values of )7, 7;, the first case of (24) applies, and it gives us a game where leader i solves](https://figures.academia-assets.com/118245873/table_010.jpg)
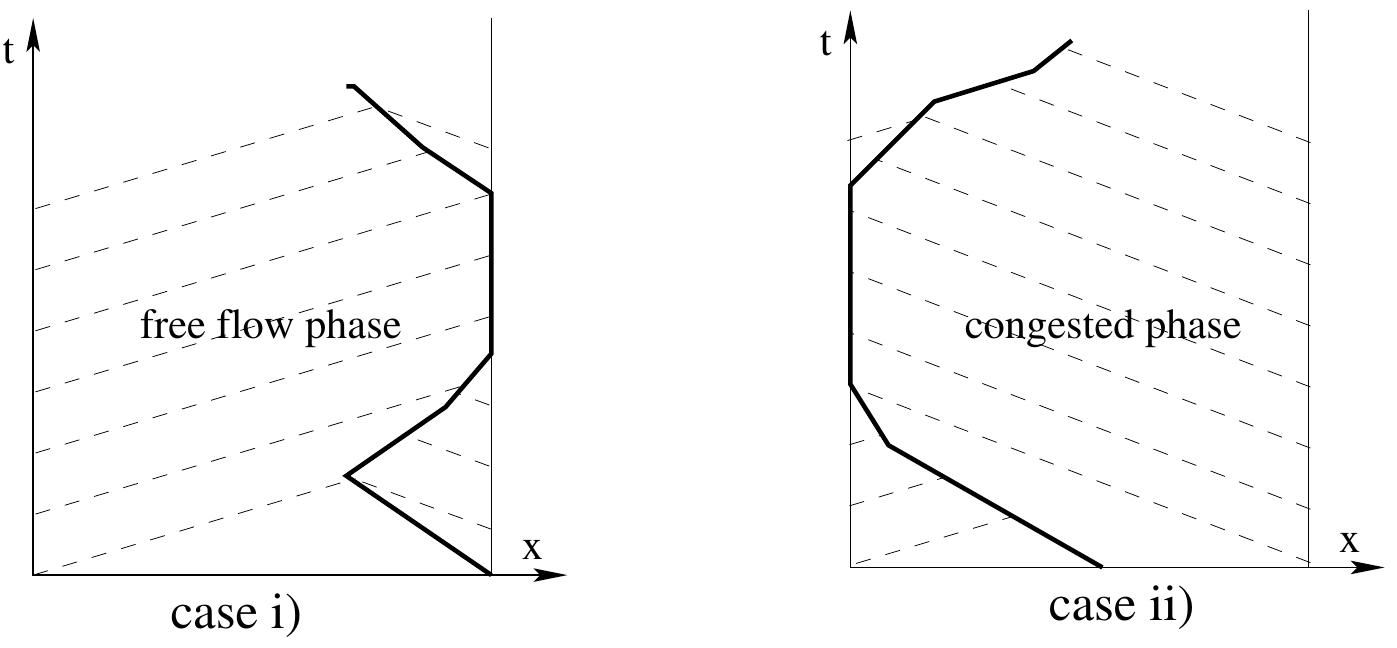
![Figure 2: A signalized junction with two incoming links and two outgoing links. In this section, the signal control problem is formulated with LKWM. We start with a single junction, with two incoming links 1, 2, and two outgoing links J3, I, (Figure 2). Each link is represented by a spatial interval [a;, b;], i = 1, 2, 3, 4. The fundamental diagrams for each Traffic signal control problem based on the LK WM](https://figures.academia-assets.com/110785962/figure_002.jpg)







![Fig. 1. Idealized moment-rotation law. Kaneko formulation [5] The M-R laws for n-critical sections are presented in the following set of equations](https://figures.academia-assets.com/107790346/figure_001.jpg)


![The new algorithm incorporates a test for identify- ing the occurrence of a plastic collapse mechanism. Such collapse is possible when the slope of the third segment of the M-R law is horizontal and occurs when a sufficient number of plastic hinges are formed to transform the structure into a mechanism before the limiting rotation is reached at any critical section. Computationally, this is detected when submatrix Ze, becomes singular [7] (see step 1 below).](https://figures.academia-assets.com/107790346/figure_004.jpg)