Key research themes
1. How can online and incremental approaches improve convex optimization in complex or data-driven environments?
This theme focuses on online convex optimization methods designed for settings where the model or environment is initially unknown or evolves over time, necessitating algorithms that learn from partial, noisy, or streaming data. Such approaches enable robust optimization despite uncertainty and incomplete information, crucial for modern machine learning, control, and signal processing applications.
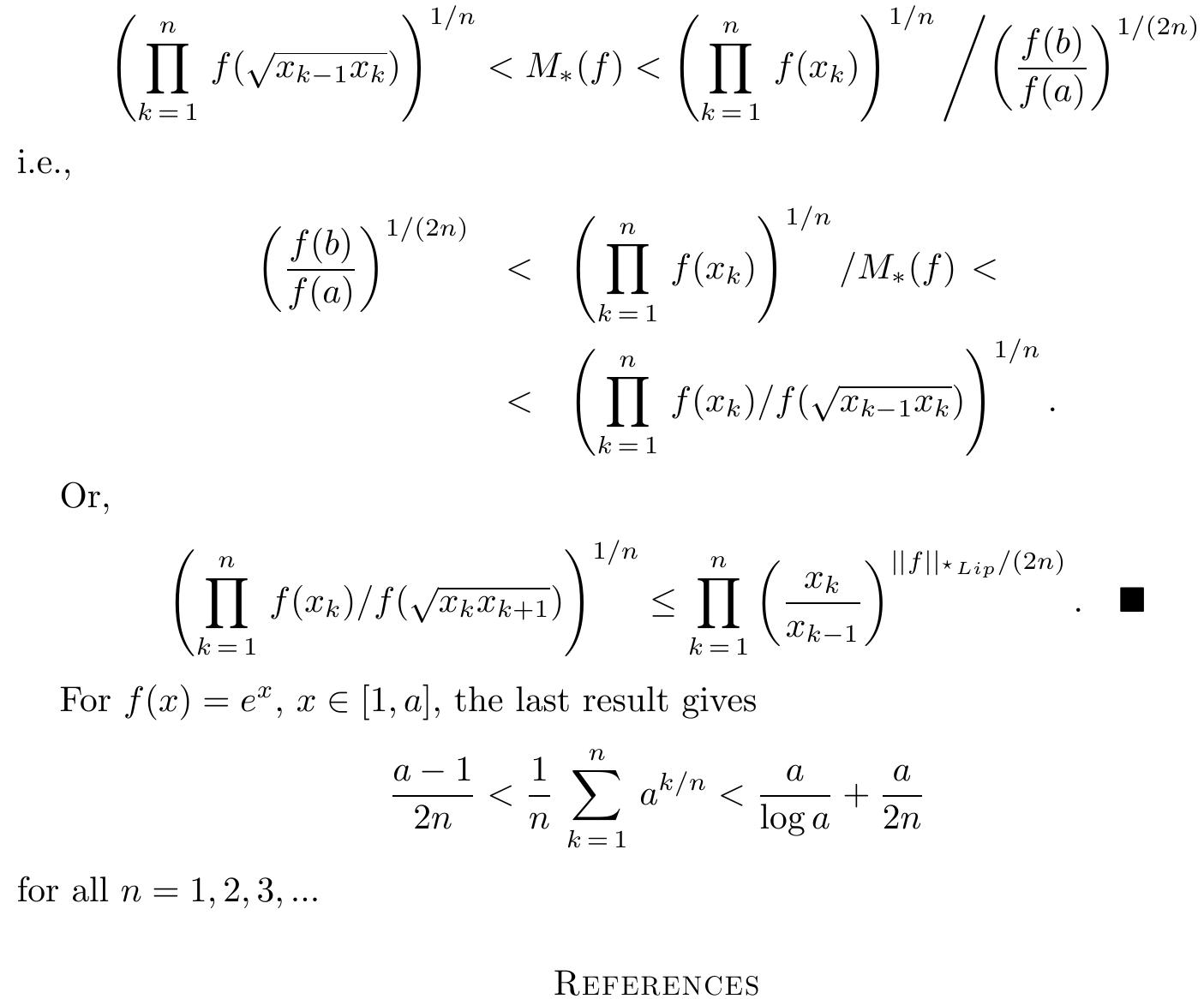
2. What are the advancements in convex analysis related to generalized convex functions and their inequalities, and how do these extensions enable tighter bounds and applications?
This theme explores the expansion of convex function theory to generalized settings such as multiplicative convexity, p-convexity, and convex functions of multiple variables through novel judgment criteria and inequalities (e.g., Hermite-Hadamard, Young's and Fejér-type). These developments provide analytical tools for deriving sharper inequalities, refining optimization bounds, and broadening the applicability of convex analysis in mathematical inequalities, functional analysis, and economic modeling.
3. How can convex quadratic optimization problems with indicator variables be convexified and efficiently solved?
This theme deals with the convex hull characterization of mixed-integer quadratic optimization problems that include both convex quadratic objectives and indicator (0-1) variables under arbitrary constraints. Understanding the structure and formulating strong convex relaxations are fundamental to solving these NP-hard problems effectively, which appear frequently in statistics, portfolio optimization, and control applications.
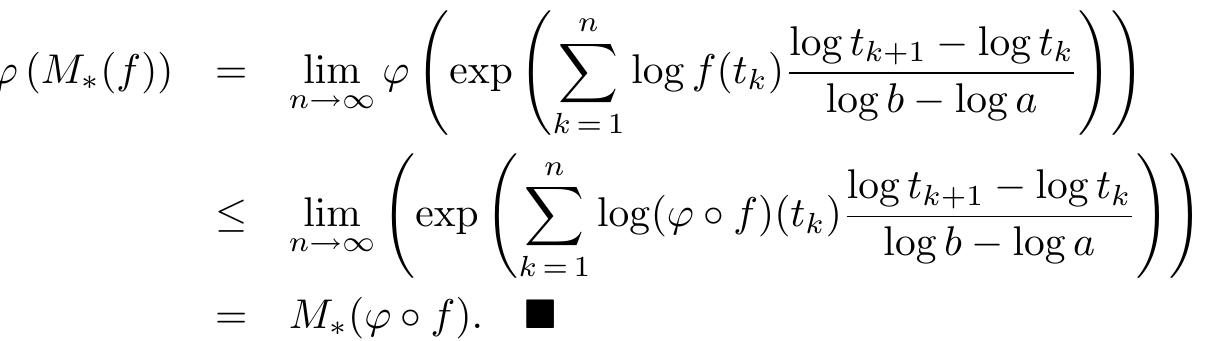
![The same argument, applied to the multiplicatively concave functions sin 3* anc cos 2% (cf. [8], p.159) gives us for every a € (0,1); they should be added to a number of other curiosities noticed recently by G. J. Tee [14]. The following result answers the question how fast is the convergence which makes the subject of Theorem 4.1 above:](https://figures.academia-assets.com/115913963/figure_002.jpg)












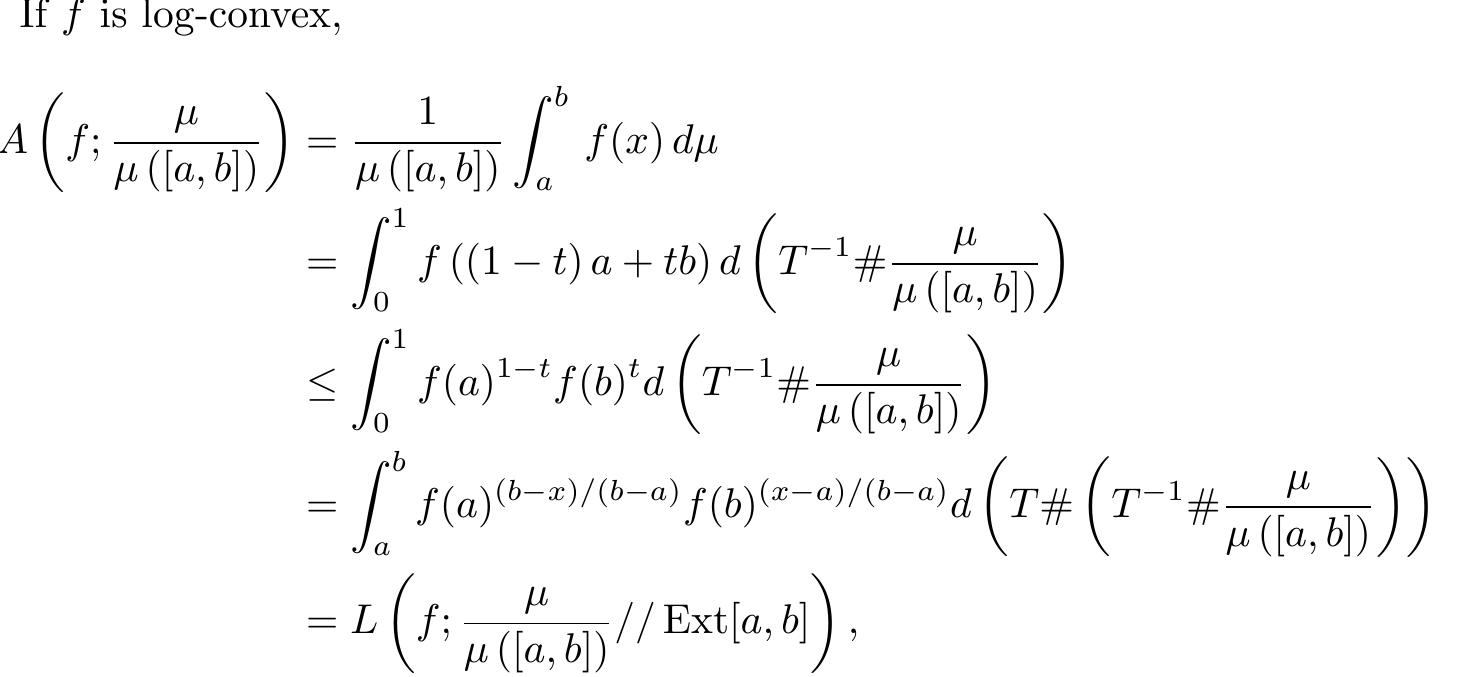
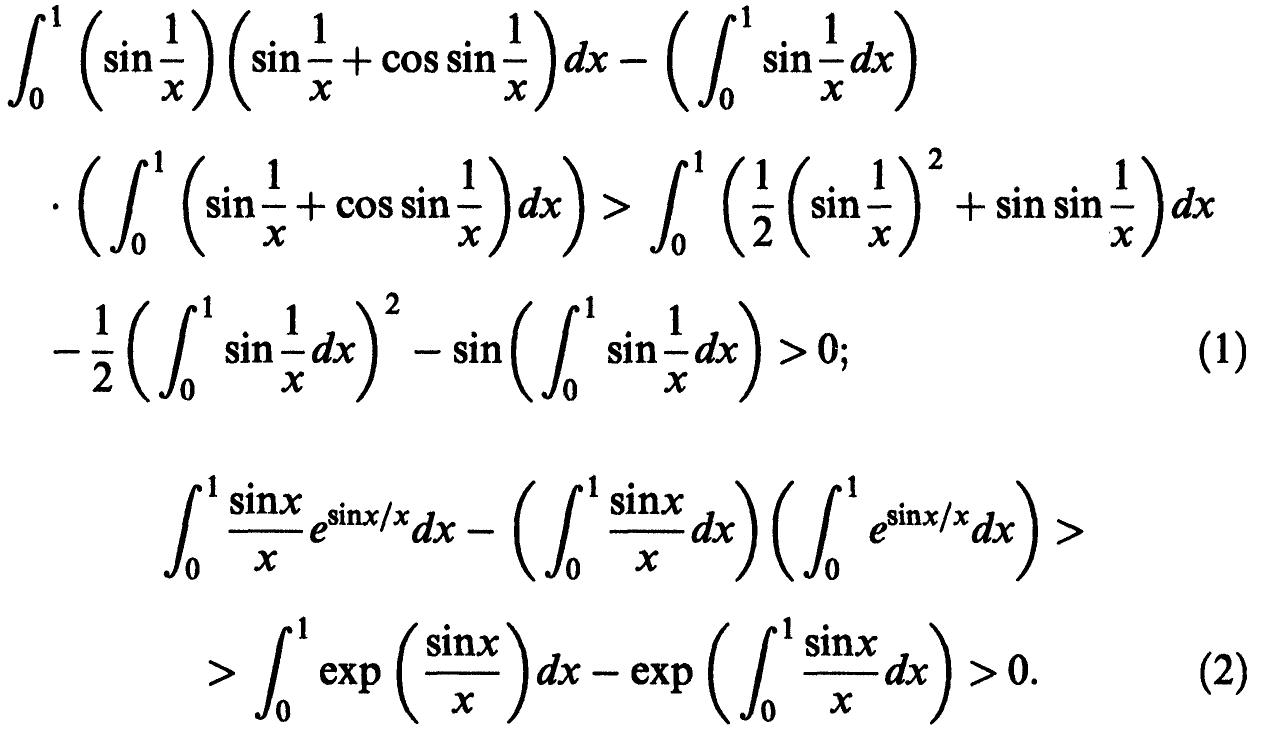
![Lemma 1.4. Fix J = [a,b], letu,A © CU, Rs), h € C(Rz, Riz), and c € R,, and let {Ax} a sequence of positive real numbers. If u(J) CI C Ry and We first establish a necessary and sufficient condition for oscillation of solutions of (1.1) when T(t) <t.](https://figures.academia-assets.com/91380156/figure_001.jpg)






![A natural question is whether Popoviciu’s inequality works for an arbitrary (M, N)-convex function. for all p,q >0 and X€ [0,1]. In this case, Popoviciu’s inequality becomes](https://figures.academia-assets.com/90375666/figure_003.jpg)


